Many studies rely on the first moment (mean) of historical asset return distributions and/or the second moment (variance or standard deviation) to predict future returns. Are the third (skewness, indicating left-right tail asymmetry) and fourth (kurtosis, indicating fat-tailedness) moments of return distributions useful for predicting returns? In the July 2011 update of their paper entitled “Do Realized Skewness and Kurtosis Predict the Cross-Section of Equity Returns?”, Diego Amaya, Peter Christoffersen, Kris Jacobs and Aurelio Vasquez investigate whether decile sorts of individual stocks based on variance, skewness and kurtosis of intraday stock returns over the past week significantly predict returns the next week. Using past-week averages of daily realized volatility, skewness, and kurtosis computed from prices at five-minute intervals, and associated firm characteristics, for a broad sample of U.S. stocks over the period January 1993 through September 2008 (over two million firm-week observations), they find that:
- The relationship between moments of intraday returns over the past week and returns the next week is:
- Strongly negative for skewness.
- Positive for kurtosis.
- Null for volatility.
- A trading strategy that each Tuesday buys (sells) with equal weighting stocks in the lowest (highest) tenth of realized skewness generates an average weekly gross return of 0.43%. Adjusting for market, size, book-to-market and momentum factors produces a gross weekly alpha of 0.46%.
- The effect is more pronounced for small companies with low book-to-market ratio, low lagged returns, high volatility (see chart below), high illiquidity, high maximum return over the previous month, low number of following analysts and high market beta.
- A strategy that each Tuesday buys with equal weighting stocks in the highest (lowest) tenth of realized kurtosis generates an average weekly gross return of 0.16%. Adjusting for market, size, book-to-market and momentum factors produces a gross weekly alpha of 0.13%.
- Results are generally robust to different measures of skewness and kurtosis, subsamples, exclusion of Januaries and portfolio weightings (though value weighting reduces performance).
The following chart, taken from the paper, summarizes the effect of realized volatility on the weekly return spread between stocks with low and high short-term skewness. The 25 average portfolio returns shown (in basis points) derive from double quintile sorts first on past-week skewness and then on past-week volatility. Results show that the skewness premium is almost non-existent for low-volatility stocks and most pronounced for high-volatility stocks.
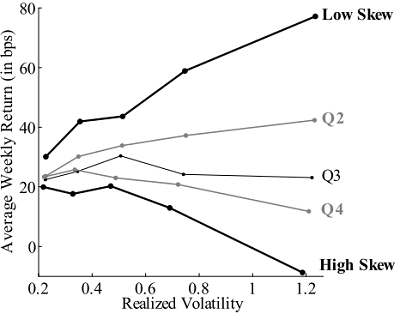
In summary, evidence indicates that U.S. stock traders may be able to exploit high-frequency return distribution skewness (especially among high-volatility stocks) and kurtosis measurements for short-term trading.
Cautions and considerations regarding findings include:
- Monitoring high-frequency returns requires intensive data collection and calculations.
- Reported returns are gross, not net. Including reasonable weekly trading frictions would materially reduce or eliminate trading returns. Note that stocks contributing most to the effects are likely the most expensive to trade.
- Tests of statistical significance assume well-behaved return distributions. To the extent the distributions are wild, these tests lose meaning.
- It would be interesting to know whether the extreme stock market conditions of late 2008 through early 2009 affect findings and whether findings hold for asset classes as well as individual U.S. stocks.
For a different take, see “Basic Equity Return Statistics”, which describes considerable variation in return distribution moments (using daily rather than high-frequency data) for stock indexes (rather than individual stocks) over long periods.