Smoothness vs. Lag Time for Moving Averages

How do moving averages work for timing asset prices, and how do different kinds of moving averages work differently? In his October 2016 paper entitled “Moving Averages for Market Timing”, Valeriy Zakamulin presents in three chapters: (1) financial series trend detection and turning point identification using moving averages; (2) the mathematics and properties of moving averages, with focus on smoothness and lag time; and, (3) types of moving averages, including regular moving averages, moving averages of moving averages and mixed moving averages that suppress lag time, with focus on differences in smoothness and lag time. Based on mathematical analyses, he concludes that:

• The longer the averaging window, the smoother the moving average (the better the removal of noise and avoidance of spurious signals), but the greater the lag time between an actual change in price trend and the associated moving average turning point. The optimal averaging window is a trade-off between smoothness and lag time.
• Moving average types differ in the way they weight past prices, and differences in weighting  approaches (for a given averaging window) produce differences in smoothness and lag time. In general:
  • The more even the weighting of past prices, the smoother the moving average.
  • The stronger the weighting of the most recent past prices, the smaller the lag time. Smoothness and lag time therefore relate inversely.
• Moving averages that overweight the most recent prices provide a more efficient trade-off between smoothness and lag time than does equal weighting (see the chart below). However, this superior efficiency may not translate into a significant advantage in practical applications.

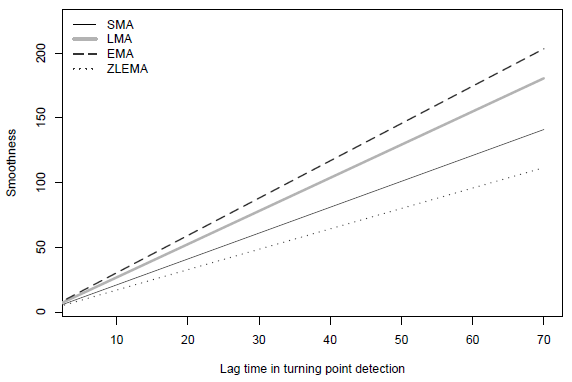
The following chart, taken from the paper, summarizes relationships between smoothness and turning point identification lag time for four kinds of moving averages:

1. SMA – Simple Moving Average (past prices weighted equally).
2. LMA – Linear Moving Average (most recent past prices weighted linearly higher than older past prices).
3. EMA – Exponential Moving Average (most recent past prices weighted exponentially higher than older past prices), with information in older prices discarded more quickly than with LMA.
4. ZLEMA – Zero Lag Exponential Moving Average, a linear combination of two EMAs that has negative weights on older past prices.

Results suggest that EMA offers the best trade-off between smoothness and lag time in turning point identication, followed by LMA and then SMA. ZLEMA offers the worst trade-off, despite its construction to suppress lag time.

In summary, theory suggests that EMA may have an inherent advantage over LMA and SMA with respect to the trade-off between moving average smoothness and lag time between actual trend change and moving average turning point.

Cautions regarding findings include:

• The paper is theoretical in nature and does not include any applications of concepts to asset timing. See the research listed below for practical applications.
• As noted in the paper, the theoretical superiority of EMA over LMA and SMA may not translate into material practical superiority.

For related research on the use of moving averages for market timing by the same author, see:

• Challenging SMA Effectiveness for Stocks
• Long-run Moving Average Horse Race for Timing the U.S. Stock Market
• Best Moving Average Weighting Scheme for Market Timing?
• Market Timing with Moving Averages Over the Very Long Run
• Net Performance of SMA and Intrinsic Momentum Timing Strategies