Can simple moving average (SMA) rules tell investors when it is prudent to leverage the U.S. stock market? In their March 2016 paper entitled “Leverage for the Long Run – A Systematic Approach to Managing Risk and Magnifying Returns in Stocks”, Michael Gayed and Charles Bilello augment conventional U.S. stock market SMA timing rules by adding leverage while in equities. Specifically, they test a Leverage Rotation Strategy (LRS) comprised of the following rules:
- When the S&P 500 Total Return Index closes above its SMA, hold the index and apply 1.25X, 2X or 3X leverage to magnify returns.
- When the S&P 500 Total Return Index closes below its SMA, switch to U.S. Treasury bills (T-bills) to manage risk.
They focus on a conventional 200-day SMA (SMA200), but include some tests with shorter measurement intervals to gauge robustness. They ignore costs of switching between stocks and T-bills. They apply targeted leverage daily with an assumed 1% annual cost of leverage, approximating current expense ratios for the largest leveraged exchange-traded funds (ETF) that track the S&P 500 Index. Using daily closes of the S&P 500 Total Return Index and T-bill yields during October 1928 through October 2015, they find that:
- SMAs effectively identify stock market volatility and trending states. For example, over the entire sample period, for the S&P 500 Total Return Index above (below) its SMA200:
- Annualized return is +14.1% (-2.3%), with annual volatility 14.7% (26.5%).
- Likelihood of a streak of four positive daily returns is 10% (5%).
- Gross annual Sharpe ratios (maximum drawdowns) over the entire sample period are (see the table below):
- 0.30 (-86%) for buying and holding the S&P 500 Total Return Index.
- 0.27 (-99%) for buying and holding the index with constant daily 2X leverage costing 1% per year.
- 0.60 (-50%) for using the SMA200 trading rules on the index without leverage.
- 0.51 (-78%) for using the SMA200 LRS trading rules on the index with 2X daily leverage costing 1% per year.
- LRS trading rules boost gross cumulative performance substantially over the sample period (see the chart below).
- LRS outperforms unleveraged buy-and-hold on a gross basis during 80% of rolling 3-year periods and suffers smaller maximum drawdowns during the four worst bear markets.
- However, over much of the sample period, high trading frictions and cost of leverage would have hampered LRS performance. Today, investors can most cheaply implement LRS with S&P 500 Index leveraged ETFs.
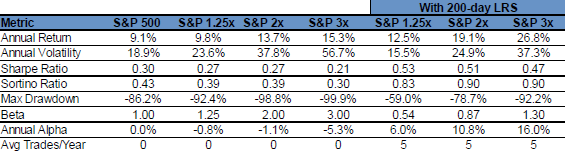
The following table, taken from the paper, summarizes gross performance of seven strategies. The first four strategies buy and hold the S&P 500 Total Return Index with 1X, 1.25X, 2X or 3X leverage. The remaining three are SMA200 LRS (an average of about five stocks-cash switches per year) with 1.25X, 2X or 3X leverage applied to the S&P 500 Total Return Index. Assumed cost of leverage is 1% per year in all cases. Results indicate that, compared to buy-and-hold with the same leverage, LRS as specified achieves: higher gross return, lower volatility, higher gross Sharpe and Sortino ratios, lower maximum drawdown, lower beta, and much stronger (and positive) gross alpha.
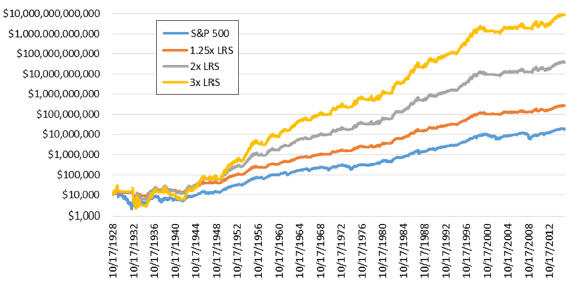
The following chart, also from the paper, compares growth of $10,000 initial investments during October 1928 through October 2015 for the S&P 500 Total Return Index and the above three SMA200 LRS scenarios. Terminal values are $19 million for the index and $270 million, $39 billion and $9 trillion, respectively, for the increasingly leveraged LRS scenarios.
Said differently, a $10,000 investment in SMA200 LRS with 3X leverage applied to the S&P 500 Total Return Index in October 1928, with 1% annual cost of leverage, grows to about half of total S&P 500 Index market capitalization in October 2015.
In summary, evidence suggests that investors may be able to improve the performance of an investment in the broad U.S. stock market by combining leverage with SMA trading rules.
Cautions regarding findings include:
- While acknowledging that the implementation costs would have been much higher than today for much of the sample period, the authors employ an assumption of 1% annual cost of leverage (based on current leveraged ETF fees) and ignore strategy switching frictions. This approach:
- Overstates realistic backtest performance.
- Ignores feedback to the market that cheap trading/leverage would have provided. The chart above suggests that the strategy could have been very disruptive, extracting so much wealth from trading counterparties that they might have left the market.
- The sample start date just before the Great Depression is highly favorable to the performance of SMA trading rules.
- Using an index overstates estimated returns by ignoring costs of maintaining a liquid fund (such as a mutual fund or ETF). Such costs are material for much of the sample period.
- In the early part of the sample period, slower data collection/processing may have affected performance of SMA rules by forcing delays between SMA signal generation and trade execution.