Does mean-variance optimization reliably beat simple equal weighting? In his August 2012 paper entitled “The Efficiency of Mean-Variance Optimization with In-depth Covariance Matrix Estimation and Portfolio Rebalancing”, Joonas Hämäläinen tests how many of 96 different mean-variance optimization implementations based on daily data outperform simple equal weighting after accounting for trading frictions. He considers three methods of determining weights for minimum variance portfolios. For each method, he considers three historical intervals for estimating optimal portfolio weights (20, 60 and 250 trading days). He considers three fixed-interval (5, 20 and 60 trading days) and one threshold-based rebalancing rules. His benchmark strategy is equal weight, rebalanced weekly (EW). He tests strategy combinations on four sets of asset returns in euros constructed from 23 MSCI country indexes: 11 European Monetary Union markets during June 2002 through May 2006 (EMU1) and during June 2006 through May 2010 (EMU2); and, 12 big emerging markets during June 2002 through May 2006 (BEM1) and during June 2006 through May 2010 (BEM2). He assumes constant trading frictions of 0.2% (0.4%) of traded value for EMU (BEM) data sets. He focuses on annualized net Sharpe ratio (with risk-free rate zero) and portfolio turnover as critical evaluation metrics. Using daily country total return index levels during June 2001 through May 2010, with out-of-sample tests commencing June 2002, he finds that:
- Turnover for EW is very low, with little sensitivity to rebalancing frequency. Rebalancing every five trading days generates the highest average Sharpe ratio (0.62) across the four sets of returns.
- Minimum variance portfolios generally have higher turnover than EW.
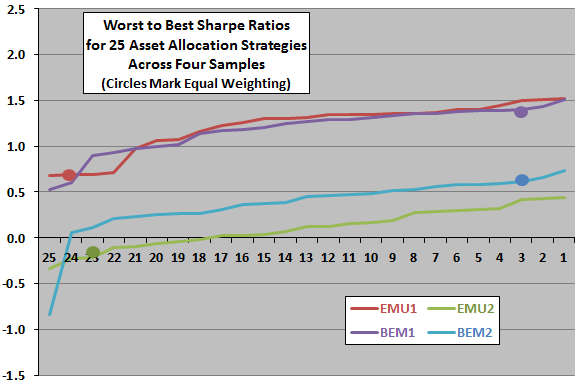
- Minimum variance portfolio performance relative to EW is mixed (see the chart below):
- 23 (22) of 24 minimum variance combinations beat EW for the EMU1 (EMU2) data sets.
- Two (two) of 24 mean-variance optimization combinations beat EW for the BEM1 (BEM2) data sets.
- Most minimum variance portfolios do have lower return standard deviations than EW.
- Based on raw predictive power, the optimal interval for estimating minimum variance portfolio weights is different for each dataset and rebalancing frequency, with short intervals yielding more accurate predictions than long intervals in most cases. However, short estimation intervals generate much higher turnover, such that medium and long estimation intervals produce the best portfolio outcomes. Overall, the 60-day historical interval beats the 20-day and 250-day intervals based on net Sharpe ratio.
- The best-performing portfolios entail relatively infrequent rebalancing to suppress trading frictions, with the threshold method most flexible.
- Picking the best estimation interval and the best rebalancing frequency appears to be more important than choosing the best estimation method.
The following chart, constructed from data in the paper, ranks the net Sharpe ratios generated by 24 minimum variance portfolios and the EW benchmark from lowest to highest for each of the four sets of stock index returns. Circles of matched colors indicate the position of the EW benchmark.
Results indicate that the EW benchmark is among the worst (best) for the EMU (BEM) samples, suggesting that the power of mean-variance optimization depends on sample properties. A possible interpretation is that mean-variance optimization works better when selected assets exhibit relatively high mutual return correlations, suggesting that the methodology may not be attractive for highly diversified assets.
In summary, evidence suggests that mean-variance optimization is sometimes superior to equal weighting and sometimes not, depending mostly on the set of assets considered.
Cautions regarding findings include:
- The study assigns no costs to the data collection and calculation burdens associated with minimum variance strategies.
- The study does not account for the data snooping bias associated with consideration of 24 combinations of minimum variance weighting estimation methods, estimation intervals and rebalancing frequencies for each set of data. Additional snooping bias may accrue to threshold rebalancing parameter selection. The aggregate bias may affect findings.
- Investors with relatively small portfolios may not be able to achieve assumed levels of trading friction, making EW relatively more attractive.
- While the study addresses trading frictions associated with rebalancing among indexes, it does not consider the costs (trading frictions and management fees) of creating tradable assets from indexes. These latter costs may vary materially across markets.
- Use of the Sharpe ratio as critical discriminator assumes well-behaved return distributions.
- The study considers only equities. Findings may not apply to sets of assets including other classes.