Trading rules that generate clustered signals present capital allocation problems. Sometimes unpredictable scarcity of signals idles capital, and other times unpredictable clustering of signals presents too many opportunities to exploit. Portfolio-level performance therefore falls considerably short of trade-level promise. Are there ways to optimize capital allocation for such trading rules? In his paper entitled “Buying Power – The Overlooked Success Factor”, winner of the 2011 Wagner Award presented by the National Association of Active Investment Managers, Thomas Krawinkel examines the interplay of capital constraints and clustered trading signals. Using example trading rules for illustration, he concludes that:
- A trader’s maximum number of open positions (MPT) is a function of initial stop loss percentage (Rs), fraction of capital risked per trade (Rp) and broker margin requirement (MR). Specifically, MPT = Rs/(Rp*MR). Note that MR=1 for a trader eschewing margin.
- Because MR is typically lower (i.e., leverage can be higher) for trades closed within a day, day traders can exploit this relationship advantageously (with respect to trading frictions and margin interest) compared to traders who hold over longer intervals. However, elevated leverage carries crash risk.
- Trading rules that cluster signals may force skipping of signals by sometimes exceeding a trader’s MPT. Random skipping of trades effectively reduces sample size and elevates trade-level volatility. Skipping more than a small fraction of signaled trades (say 5%) can degrade a trading rule to the point of uselessness.
- A spreadsheet tool (provided with the paper) automates sensitivity testing of MPT input parameters and trading rule settings, with “trade load” (buying power utilization, or likelihood that capital constraints will cause signal skipping) as a key output. A low trade load is desirable to cope with signal clusters.
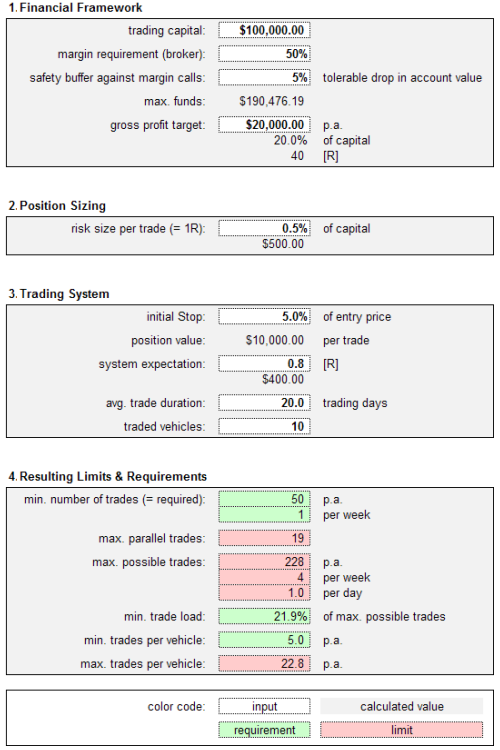
The following chart, taken from the paper, depicts the “Quick Check” tool (populated with example data), which facilitates sensitivity testing of capital constraint parameters (blocks 1 and 2) and trading rule settings (block 3). Block 4 provides feedback on the feasibility of achieving a specified profit goal based on a specified allocation/trading system. For example:
- Increasing average trade duration increases trade load (likelihood of skipping signals).
- Decreasing risk per position increases number of trades required to achieve the profit goal and increases trading friction.
- Adding trading vehicles increases trade load (likelihood of skipping signals).
In summary, traders should be sensitive to the interplay of capital constraint parameters and trading rules that generate signal clusters.
Cautions/amplifications regarding findings include:
- Testing of different capital constraint parameters and trading rule settings on the same trading rule (as facilitated by the “Quick Check” tool) introduces data snooping bias, thereby overstating the performance of the best set of parameters/settings.
- While a low “trade load” is desirable from the standpoint of exploiting trade signal clusters, a low load also indicates idle capital.
- As implied by an example in the paper, the best signals of trading strategies (those with the highest returns) may well tend to cluster, and the very best signals may come late within clusters. In other words, the very best trades are the least accessible to real, capital-constrained execution. In this scenario, skipping trades due to capital constraints not only increases trade-level return volatility but also decreases average return per trade, a double hit to portfolio performance.
- Statistical inference in the paper generally assumes tame (such as Gaussian, or normal) trading rule return distributions. To the extent that actual return distributions are wild, this reasoning loses power.
See “Review of Larry Connors’ Daily Battle Plan” for a “real life” example of bridging from trade-level statistics to portfolio-level performance via simple capital constraints applied to a sequence of trade signals. This example finds that the best signals tend to come late within clusters.