How does use of actuarial estimates of retiree longevity and empirical mean reversion of stock market returns affect estimated retirement portfolio success rates? In the October 2018 revision of his paper entitled “Joint Effect of Random Years of Longevity and Mean Reversion in Equity Returns on the Safe Withdrawal Rate in Retirement”, Donald Rosenthal presents a model of safe inflation-adjusted retirement portfolio withdrawal rates that addresses: (1) uncertainty about the number of years of retirement (rather than the commonly assumed 30 years); and, (2) mean reversion in annual U.S. stock market returns (rather than a random walk). He estimates retirement longevity as a random input based on the Social Security Administration’s 2015 Actuarial Life Table. He estimates stock market real returns and measures their mean reversion using S&P 500 Index inflation-adjusted total annual returns during 1926 through 2017. He models real bond returns using 10-year U.S. Treasury note (T-note) total annual returns during 1928 through 2017. He applies Monte Carlo simulations (3,000 trials for each scenario) to assess retirement portfolio performance by:
- Assuming an initial retirement portfolio either 100% invested in stocks or 60%/40% in stocks/T-notes (rebalanced at each year-end).
- Debiting the portfolio each year-end by a fixed, inflation-adjusted percentage of the initial amount.
- Calculating percentage of simulation trials for which the portfolio is not exhausted before death (success) and average portfolio terminal balance for successful trials.
He considers two benchmarks: (1) no stock market mean reversion (random walk) and fixed 30-year retirement; and, (2) no stock market mean reversion and actuarial estimate of retirement duration. He also runs sensitivity tests to see how changes in assumptions affect success rate. Using the specified data, he finds that:
- Average longevity for a male age 65 based on 1,000 simulations is 18 years, far shorter than the typical assumption of 30 years of retirement.
- An optimal mean reverting model of S&P 500 Index annual returns generates rolling window returns much more like reality than does a random walk model. T-note returns do not exhibit mean reversion.
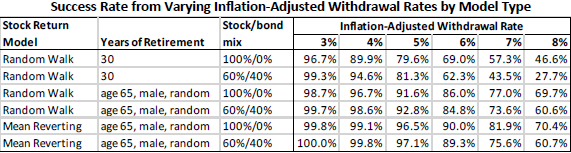
- For a male retiring at age 65 with a 100% allocation to stocks (see the table below):
- Fixed 30-year retirement duration, random annual stock market returns and a 4% annual withdrawal rate have 90% success rate.
- Replacing the 30-year duration with actuarial longevity increases success rate for a 4% withdrawal rate to 97%.
- Further replacing random stock market returns with mean reverting returns increases success rate for a 4% withdrawal rate to 99%. Success rate for a 6% withdrawal rate is 90%.
- With actuarial longevity and mean reverting stock market returns, T-notes are less helpful in supporting modest withdrawal rates than with conventional assumptions.
- Lowering the observed 6.9% compound annual growth rate for the stock market to 4%, using actuarial longevity and mean reverting stock market returns, generates a 95% success rate for a 4% withdrawal rate.
- Retiring before age 65 or being female generally decreases success rate due to increased longevity.
The following table, taken from the paper, summarizes success rates for 36 retirement scenarios (six sets of retirement/portfolio assumptions times six annual withdrawal rates) as modeled above. In general, using actuarial longevity (“random”) to estimate years of retirement and using mean reversion when modeling stock market returns both boost retirement portfolio success rates.
In summary, simulation indicates that using actuarial longevity to estimate retirement duration and optimally accounting for mean reversion in stock market returns generate higher retirement portfolio success rates than do conventional modeling assumptions.
Cautions regarding findings include:
- The test of stock market return mean reversion is in-sample with respect to both the test of mean reversion and the retirement simulations. In other words, data used for testing are the same data used to quantify mean reversion parameters. An investor operating in real time would not know these parameter values, and an out-of-sample test may not convincingly show predictable mean reversion.
- Actuarial data is similarly somewhat in-sample. Future actuarial data may differ.
- Actual funds with frictions and fees may not reliably capture S&P 500 Index and T-note returns.
- Samples of stock market and T-note returns are short in terms of the modeled number of independent retirements, undermining confidence in findings.