Net Performance of SMA and Intrinsic Momentum Timing Strategies

Does stock market timing based on simple moving average (SMA) and time-series (intrinsic or absolute) momentum strategies really work? In the November 2013 version of his paper entitled “The Real-Life Performance of Market Timing with Moving Average and Time-Series Momentum Rules”, Valeriy Zakamulin tests realistic long-only implementations of these strategies with estimated trading frictions. The SMA strategy enters (exits) an index when its unadjusted monthly close is above (below) the average over the last 2 to 24 months. The intrinsic momentum strategy enters (exits) an index when its unadjusted return over the last 2 to 24 months is positive (negative). Unadjusted means excluding dividends. He applies the strategies separately to four indexes: the S&P Composite Index, the Dow Jones Industrial Average, long-term U.S. government bonds and intermediate-term U.S. government bonds. When not in an index, both strategies earn the U.S. Treasury bill (T-bill) yield. He considers two test methodologies: (1) straightforward inception-to-date in-sample rule optimization followed by out-of-sample performance measurement, with various break points between in-sample and out-of-sample subperiods; and, (2) average performance across two sets of bootstrap simulations that preserve relevant statistical features of historical data (including serial return correlation for one set). He focuses on Sharpe ratio (including dividends) as the critical performance metric, but also considers terminal value of an initial investment. He assumes the investor is an institutional paying negligible broker fees and trading in small orders that do not move prices, such that one-way trading friction is the average bid-ask half-spread. He ignores tax impacts of trading. With these assumptions, he estimates a constant one-way trading friction of 0.5% (0.1%) for stock (bond) indexes. Using monthly closes and dividends/coupons for the four specified indexes and contemporaneous T-bill yields during January 1926 through December 2012 (87 years), he finds that:

• Based on the straightforward in-sample/out-of-sample method:
  • Over the entire sample period, the optimal in-sample measurement interval varies by index and strategy type (see the first table below).
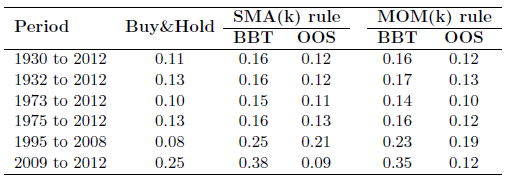
  • The best trading rule generally outperforms buy-and-hold the passive benchmark on a gross, in-sample basis. On a net out-of-sample basis, however, results are mixed. For the S&P 500 Composite Index (see the second table below), severe bear markets in 1930-31, 1973-74, 2001-02 and 2007-08 drive outperformance of the market timing strategies. Timing performance relative to buy-and-hold during a subperiod depends largely on whether it contains one or more of these severe bear markets. The timing strategies for the stock indexes underperform buy-and-hold throughout the 25-year period from 1975 through 1999.
  • During an out-of-sample test during 1930 through 2012, only three of eight strategy-index combinations beat their respective buy-and-hold benchmarks based on net monthly Sharpe ratio. Specifically, the SMA strategy boosts net Sharpe ratio for the S&P Composite Index by 10%, the intrinsic momentum strategy boosts net Sharpe ratio for the S&P Composite Index by 12%, and the SMA strategy boosts net Sharpe ratio for intermediate-term U.S. government bonds by 10%.
• Based on more elaborate bootstrap testing:
  • Only two of eight strategy-index combinations reliably beat their respective buy-and-hold benchmarks based on net monthly Sharpe ratio. Specifically, the SMA strategy improves net Sharpe ratio for the S&P Composite Index by 7%, and the SMA strategy boosts net Sharpe ratio for intermediate-term U.S. government bonds by 8%.
  • In about 80% of the intervals between an exit signal and the next entry signal, the market timing strategies underperform buy-and-hold.
  • The stronger the serial correlation of returns for an index, the better the expected performance of a market timing strategy.
  • For stock indexes, timing strategy return distributions usually have fatter left tails and thinner right tails than those for buy-and-hold. In other words, timing strategies may elevate rather than suppress downside risk.

The following table, taken from the paper, summarizes optimal in-sample measurement intervals for SMA and intrinsic momentum (MOM) strategies as applied separately to the two stock indexes and two bond indexes used in the study over the entire 1926-2012 sample period. The widely used 10-month SMA is optimal for the S&P Composite Index, but not for the other three indexes. Results suggest that there is no consistent cycle underlying these indexes.

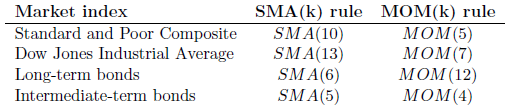
The next table, also from the paper, summarizes for various subperiods:

1. Monthly Sharpe ratios for buying and holding the S&P Composite Index (Buy&Hold).
2. Gross monthly Sharpe ratios for timing the index based on the best backtested SMA and MOM rules (BBT).
3. Net monthly Sharpe ratios for timing the index out-of-sample based on optimal preceding in-sample SMA and MOM rules (OOS).

Results suggest that it is always possible to beat the market by exploiting look-ahead bias and ignoring trading frictions, but it is difficult to beat the market under realistic conditions.

In summary, evidence suggests that SMA and intrinsic momentum timing strategies offer at best marginally better risk-adjusted performance than buy-and-hold over the long run. Over medium runs, however, the timing strategies tend to underperform buy-and-hold because their payoffs concentrate in a few relatively short historical episodes.

Cautions regarding findings include:

• The author’s assertion that the bootstrap simulation methods “preserve all relevant statistical features of the historical data series” seems difficult to prove.
• Analyses apparently assume that timing rule signal generation and consequent trade execution coincide, which may be problematic (especially early in the sample period when calculation and dissemination of information are slow and no fund proxies for the indexes exist).
• Trading frictions vary considerably over the sample period (see “Trading Frictions Over the Long Run”). The assumed level of 0.5% for equities is arguably too low for much of the sample period and too high for the latter part of the sample period.
• Use of indexes rather than tradable assets ignore costs of constructing and maintaining a liquid fund of changing components (affecting both buy-and-hold and timing strategies).
• The study ignores tax implications of market timing, which would favor buy-and-hold.

For a similar study, see “Technical Trend-following: Fighting the Last War?”.

See also “Is There a Best SMA Calculation Interval for Long-term Crossing Signals?”, “Intrinsic Momentum or SMA for Avoiding Crashes?” and “Optimal Intrinsic Momentum and SMA Intervals Across Asset Classes”.